해시맵

- 인덱스가 아닌 키를 이용하여 값을 저장하고 접근하는 자료구조
- key는 값을 해시 함수를 통해 유일한 인덱스 값으로 만들어서 접근
- 키값은 정수형이어야 한다.
- 정수형이 아닐 시 정수형으로 변경해준다.
- 가장 이상적인 해싱함수는 키들을 균등하게 충돌없이 흩어지도록 저장된다.
- 조회, 추가, 삭제가 모두 O(1)의 속도를 가진 자료구조다.
해시 함수
md5, sha512와 같은 해시함수라고 생각하면 된다. 무한대의 입력값에 대해서 유한한 길이의 인덱스 값을 계산하기 위한 함수도 해시함수다. 이때 인덱스값은 배열의 전체길이인 M보다 클 수 없다. 해시함수는 여러가지 종류가 있으며 밑에 적인 함수가 전부가 아니다.
- Mid-square함수
- 키를 제곱 후 중간값을 해시값으로 결정
- 중간값은 비트값을 기준으로 한다.
- Ex)
- 키를 제곱한 결과: 0b11111111_00000000_11111111(24bit)
- 해시: 0b00000000 => 0
- Folding 함수
- 정수의 자릿수를 나누어 연산된 결과를 해시값으로 결정
- 입력되는 키값이 매우 클 때 유리s
- Ex)
- 입력 key값: 123_456_789
- 함수: 3자리씩 끊은 정수를 n1,n2,n3라고 할 때 abs(n1+n2-n3)
- 해시값: abs(123+456-789)=210
- Division함수
- M이 소수인 해시테이블에서 테이블 크기로 나누고 나머지를 해시값으로 사용
- 인덱스 범위: 0 ~ M-1
- 소수를 이용하면 나눗셈 사용시 소수가 키들을 균등하게 인덱스로 변화시킨다.
충돌
해시함수의 결과는 항상 유일하지 않다. 이유는 입력값은 무한한 값이지만 해시함수의 결과는 0부터 M-1까지의 유한한 값을 제공하기 때문이다. 서로 다른 값 v1,v2가 같은 해시 함수 h(x)에 연산을 수행한 후 h(v1)=h(v2) 이면 이를 충돌이 발생했다고 한다.
예를 들어보자 배열길이 M이 10일 때 해시함수 h(x)를 다음과 같이 정의한다.
h(x)=x%M
해시맵에서 사용될 키값인 k1=10, k2=20이면 해시함수의 결과는 다음과 같다.
h(k1)=10%10=0
h(k2)=20%10=0
키값이 다름에도 해시함수의 결과가 같다. 이를 k1과 k2가 해시충돌이 발생했다고 한다.
해시충돌이 발생하면 k1이 있는 값에 k2를 덮어쓰거나 k2를 통해 값을 접근하면 k1값이 읽혀지는 문제가 발생할 수 있다. 해시맵은 이러한 문제를 해결하기 위해 2가지중 하나로 해시맵을 구성한다. 바로 개방주소 방식, 폐쇄주소 방식이다.
개방 주소 방식 해시맵(Open Addressing)
해시테이블을 열린 공간이라 가정하고 충돌이 발생할 때 충돌된 키를 일정한 규칙을 통해 충돌이 발생한 지점에서 점프하면서 비어있는 공간을 찾아 이를 키로 설정하는 방식이다.
여기서 점프하여 비어있는 공간을 찾는 방식은 여러개가 있지만 필자는 4가지만 설명하겠다.
1. 선형 조사(Linear Probing)
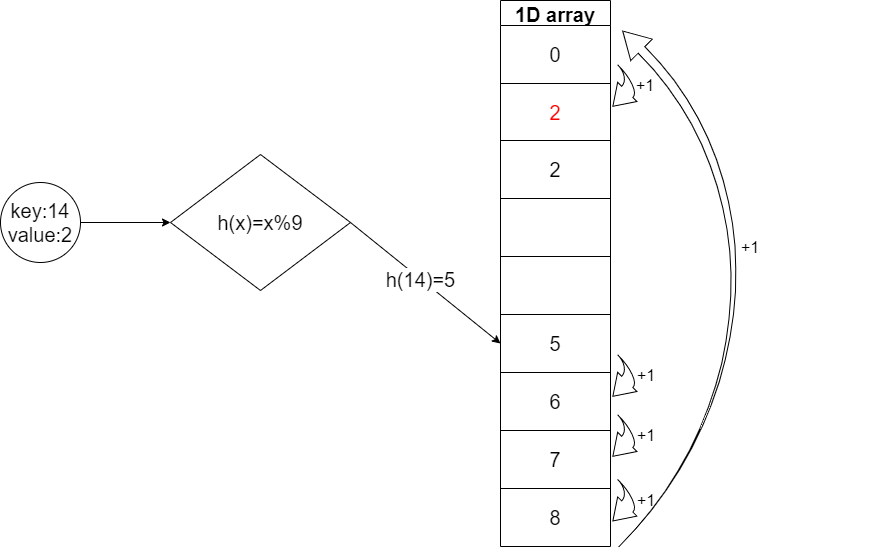
- 충돌이 발생한 원소부터 순차검색하여 최초로 발견하는 빈 공간에 충돌된 원소를 저장하는 방식
- h(key)가 i일 때 i++를 수행하면서 빈 값을 찾는다.
- i가 배열인덱스 범위를 초과할 경우 0부터 시작한다.
- 수식: (h(key)+j)%M
- 문제점: 1차 군집화 현상 발생
- 원인: 충돌이 발생된 부분에서 가장 인접한 장소의 빈공간을 찾아서 값을 삽입하여 충돌이 발생된 부분에 값이 몰린다.
참고: 1차 군집화
위의 선형조사 그림에서 해싱된 값이 5일 때 이미 해당 인덱스는 값이 존재하므로 빈 공간을 가진 인덱스를 찾기 위해 6번의 step을 이동하여 빈공간을 찾는다. 이는 배열 전체의 길이 m이 9인 것을 생각하면 배열 전체의 2/3을 탐색하므로 성능이 저하된다. 이처럼 해시 충돌이 자주 발생하는 부분에 값이 몰리는 것을 1차 군집화라고 한다.
2. 이차 조사(Quadratic Probing)
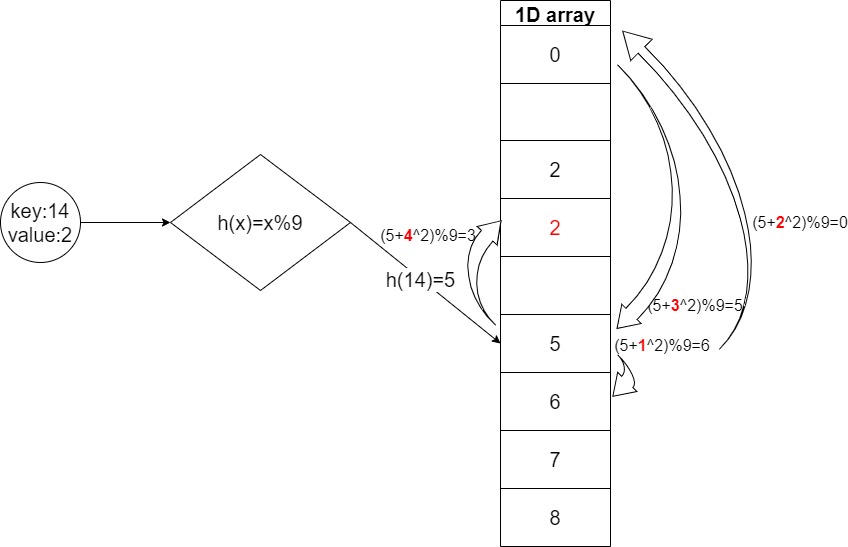
- 선형 조사에 제곱을 더한 방식
- 충돌이 발생한 인덱스가 idx일 때 (idx+1)^2를 수행한다.
- 충돌이 발생한 원소의 키를 제곱연산한 결과를 더해 빈 공간을 찾는다.
- 수식: (h(key)+j**2)%M
- 이웃된 빈곳이 채워지는 1차군집화 해결
- 이동되는 규칙이 같으므로 또 다른 형태의 군집화(2차 군집화)가 발생한다.
참고: 2차 군집화
이차조사의 그림을 보면 이동되는 순서가 정해진다. 해시값 5를 기준으로 5+(step*step)%9순으로 이동한다. 즉 선형방식에서 크기 벗어나지를 못한 것을 확인할 수 있다. 해시값이 5인 키값인 5,14,23, 즉 5+9*n의 값이 들어와 충돌이 발생할 때마다 5+1^2,5+2^2,5+3^2인덱스 순으로 순회한다. 1차 군집화처럼 인접한 위치에서 군집화가 발생하진 않지만 충돌이 발생된 키가 점프를 하면서 빈 인덱스를 찾는 과정이 동일하므로 또 다른 형태의 군집화가 발생한다. 이를 2차군집화라고 한다.
2차군집화는 또 다른 문제가 있는데 바로 빈 공간이 있음에도 불구하고 찾을 수 없다. 해시함수 h(x)=(x+i**2)%9를 사용하여 20번 조사하면 다음과 같은 인덱스를 접근한다는 것을 알 수 있다.
# print(list(map(lambda value: (5+value**2)%9,[v for v in range(1,21)])))
[6, 0, 5, 3, 3, 5, 0, 6, 5, 6, 0, 5, 3, 3, 5, 0, 6, 5, 6, 0]
결과를 보면 6, 0, 5, 3, 3, 5, 0, 6, 5, 순으로 순회한다는 것을 알 수 있다. 즉 충돌이 발생하여 원소를 순회하면서 빈공간을 찾는 과정에서 1,2,4,7,8,9의 값은 영원히 방문하지 않는다. 만약 이 공간에만 빈공간이 존재할 경우 할당가능한 공간이 존재함에도 이를 영원히 찾지 못하는 문제가 발생한다.
3. 랜덤 조사(Random Probing)
- 점프하는 간격을 랜덤으로 지정하는 방식
- 완전한 랜덤을 수행하지 않을 시 같은 시드값을 가지므로 점프시퀀스가 동일하여 랜덤한 위치에 군집이 발생할 수 있다.
- 수식: (h(key)+random_value)%M
4. 이중 해싱(Double Hashing)
2개의 해시함수를 이용하는 방법이다. 두 개의 해시함수를 h(x), g(x)라고할 때 h(x)를 키값을 해싱하여 최초로 인덱스값을 접근할 때 사용하고 g(x)는 충돌이 발생할 때 점프할 범위를 계산할 때 사용한다. 즉 충돌이 발생하지 않으면 1개의 해시함수를 쓰다가 충돌이 발생하면 해시함수를 추가적으로 사용하는 방법이다.
- 수식: (h1(key)+j*h2(key))%M 2차 해시함수g(x)는 1차 해시와 달리 다음의 조건을 만족하여야 한다.
- 0을 리턴하지 않는다.
- 해싱된 결과값과 해시테이블의 크기는 서로소이면 더 좋은 성능을 내준다.
- 1차 해시함수와 동일한 해시함수와 다른 함수이어야 한다.
베열의 크기를 소수로 맞추면 2번 조건을 맞추기 용이하다.
폐쇄 주소 방식(Closed Addressing)
충돌이 발생하면 빈 공간을 찾지 않고 충돌이 발생한 위치를 재사용한다. 즉 별도의 점프없이 해시값이 대응되는 곳에 저장한다.
폐쇄 주소 방식의 대표적인 방법은 체이닝 방식이다.

배열의 원소들은 각각 연결 리스트를 가지며 충돌이 발생할 빈 공간을 찾지 않고 연결리스트의 끝에 값을 추가한다.
재해시(Rehash)
개방 주소 방식을 사용하든 폐쇄 주소 방식을 사용하든간에 관리되는 데이터 양이 늘어나면 속도가 저하된다. 개방 주소 방식은 더 많은 점프를 통해 빈공간을 찾고 폐쇄 주소 방식은 더 긴 연결 리스트를 탐색해야 한다. 특히 폐쇄 주소 방식은 일부 데이터가 특정 연결리스트에 몰릴 수 있어서 평균적으로 데이터를 탐색하는 속도가 많이 저하될 수 있다. 반대로 관리되는 데이터양이 작지만 해시맵이 사용하는 배열의 길이가 커도 문제가 발생한다. 100_000개의 해시맵의 크기에서 10개의 데이터를 저장하고 있다면 99_990개의 빈 공간이 생긴다. 만약 int 타입의 배열이라면 99_990*4kb=399_960kb => 약 390mb의 데이터공간이 낭비된다. 즉 효율적인 탐색, 삽입, 삭제 연산과 효율적인 저장공간을 위해 데이터의 양에 따라 해시 테이블을 유동적으로 바꿀 수 있어야 한다. 이를 위해 사용하는 방법이 재해싱이다. 재해싱은 상당히 무거운 연산이므로 자주 발생하지 않는다. 적재율을 기준으로 재해싱을 할지 안할 지를 선택한다. 적재율은 다음과 같은 수식으로 구할 수 있다.
적재율=테이블에 저장된 키의 개수/현재 해시테이블의 크기
재해싱은 배열의 길이를 늘이거나 줄일 땐 기존배열을 이용할 수 없고 새로운 배열을 만들고 기존 배열의 값들을 옮긴다. 이때 배열의 길이가 달라지면서 기존 해시값들을 사용할 수 없다.
예를 들어 h(x)=(5+value)%M이라고 할 때 M이 5이고 value가 1이면 h(1)=1이다. 이때 배열의 길이를 2배로 늘리면 M=10이 되므로 h(1)=(5+1)%10=6이므로 같은 값임에도 전혀 다른 해시값을 가진다. 즉 배열을 증감할 경우 기존의 해시값들을 사용할 수 없다. 따라서 기존 배열에 들어있던 값들을 다시 해싱하여 새로운 배열에 옮겨야 한다. 그래서 재해싱의 속도는 기존의 원소 개수만큼 해시함수를 수행하므로 O(n)의 속도를 가진다.
'CS' 카테고리의 다른 글
| [Network] http (0) | 2022.12.04 |
|---|---|
| [자료구조]BST, AVL트리 (0) | 2022.07.06 |
| [자료구조] 트리 개론 (0) | 2022.07.04 |
| [Web]CORS (1) | 2022.06.20 |
| [GoF] 2. Factory (0) | 2022.03.22 |
