탐색트리
- 저장된 데이터에 CUD 연산을 수행가능한 트리 기반 자료구조
- 단순 트리는 배열이나 연결리스트를 사용하면 각 연산을 수행하는데 O(n)의 속도가 필요하므로 이를 줄이기 위함
- 트리의 구조를 이용하면서 CUD가 빈번하게 발생하는 상황에서 유리
- 종류: 이진탐색트리, AVL트리, 2-3트리, 레드블랙트리, B-트리등
이진 탐색 트리(Binary Search Tree, BST)
- 이진탐색을 트리형태로 접목한 트리
- 이진 탐색 트리의 조건
- 자식 노드는 최대 2개만 가질 수 있다.
- 왼쪽 자식 노드는 부모보다 작아야 한다.
- 오른쪽 자식 노드는 부모보다 커야 한다.
- 정렬된 형태로 데이터를 구성
- 노드를 기준으로 왼쪽 후손노드들은 기준이 되는 노드보다 작고 오른쪽 후손노드는 기준이 되는 노드보다 크다
- 중위순회로 순회할 시 값이 정렬되어 출력이 된다.
이진 트리 종류
이진 탐색 트리에서 CUD를 수행하면서 트리의 모양이 바뀐다. 어떠한 모양으로 바뀔 수 있는지를 보자.
1. 포화 이진 트리(Perfect Binary Tree)

- leaf노드를 제외한 모든 노드가 자식을 2개씩 가지는 트리
- 노드개수가 N개일 때 Depth는 logN이다.
- CRUD를 위해 값을 탐색할 때 logN의 노드만 탐색하면 수행할 수 있다.
- 같은 레벨의 노드들은 루트까지의 간선 개수가 같다.
- 가장 이상적인 이진 탐색 트리
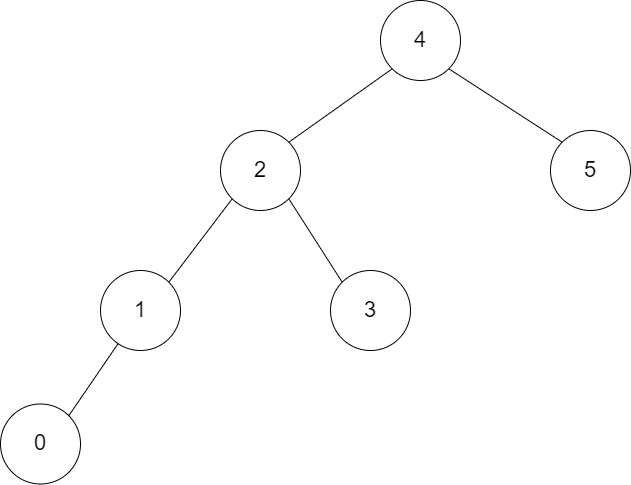
2. 편향 이진 트리(Skewed Binary Tree)

- 노드들이 특정 방향으로만 편중되어 있는 트리
- 값이 정렬되어서 삽입되어서 왼쪽 혹은 오른쪽으로 값이 편중된다.
- 노드개수가 N개일 때 depth가 N이다.
- 가장 이상적이지 않은 이진 탐색 트리
3. 완전 이진 트리(Complete Binary Tree)

- 포화이진트리에서 leaf노드들중 가장 왼쪽의 노드들부터 채워지고 오른쪽 노드가 비어있는 트리
- heap자료구조가 이용
4. 정 이진 트리(Full Binary Tree)

- 모든 노드가 자식노드를 0 혹은 2개만 가지는 트리
5. 균형 이진 트리(Balanced Binary Tree)

- 서브트리들간의 depth 차이가 최대 1까지만 차이나는 트리
AVL(Adelson-Velsky and Landis) 트리
- 삽입, 삭제를 수행할 때마다 균형을 맞춰주는 이진 탐색 트리
- AVL트리의 조건
- 단순 이진트리에서 발생할 수 있는 편향트리를 방지한다.
- 노드가 N개일 때 logN의 높이를 가져 삽입, 탐색, 삭제연산이 O(logN)으로 보장
- 삽입, 삭제 연산과정
- 이진 탐색 트리처럼 삭제 혹은 삽입연산을 수행
- 삽입, 삭제연산이 발생한 노드를 기준으로 루트노드까지 올라가면서 깊이의 불균형을 찾아서 해결
- 삽입, 삭제할 시 편향된 트리로 변경되는 것을 회전 연산으로 균형을 유지시킨다.
균형을 유지하는 방법: 회전연산
균형을 유지하기 위해 AVL트린는 2가지의 연산을 필요로 한다.
- Right 회상
- 왼쪽 서브트리가 오른쪽 서브트리보다 클 때 발생
- 왼쪽 서브트리내의 오른쪽 서브트리가 오른쪽 서브트리내의 왼쪽 서브트리로 옮겨진다.
- Left 회전
- 오른쪽 서브트리가 왼쪽 서브트리보다 클 때 발생
- 오른쪽 서브트리 내의 왼쪽 서브트리를 왼쪽 서브트리 내의 오른쪽 서브트리로 바꾼다.
균형이 깨지는 경우
삽입, 삭제로 인해 균형이 깨져버린 케이스들이다.
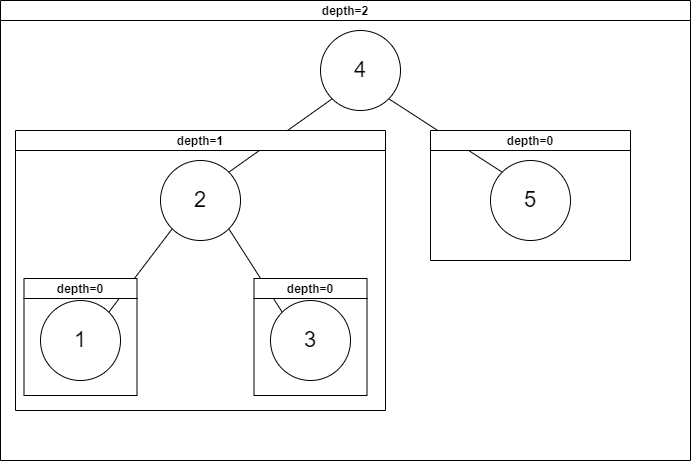
LL(Left Left)상태
- 왼쪽 서브트리내의 왼쪽 서브트리가 가장 깊다.
- 2번을 루트로 하는 서브트리의 depth: 2
- 1번을 루트로 하는 서프트리의 depth: 0
- 해결: 2번 노드를 Right연산을 수행

LR(Left Right)상태

- 왼쪽 서브트리 내의 오른쪽 서브트리가 가장 깊다.
- 2번을 루트로 하는 서브트리의 depth: 2
- 5번을 루트로 하는 서브트리의 depth: 0
- 해결책: 2번 노드를 left연산 후 3번 노드를 Right연산을 수행

RR(Right Right)상태

- 오른쪽 서브트리내의 오른쪽 서브트리가 가장 깊을 때 발생
- 1번을 루트로 하는 서브트리의 depth: 0
- 4번을 루트로 하는 서브트리의 depth: 2
- 해결책: 4번 노드를 Left연산을 수행
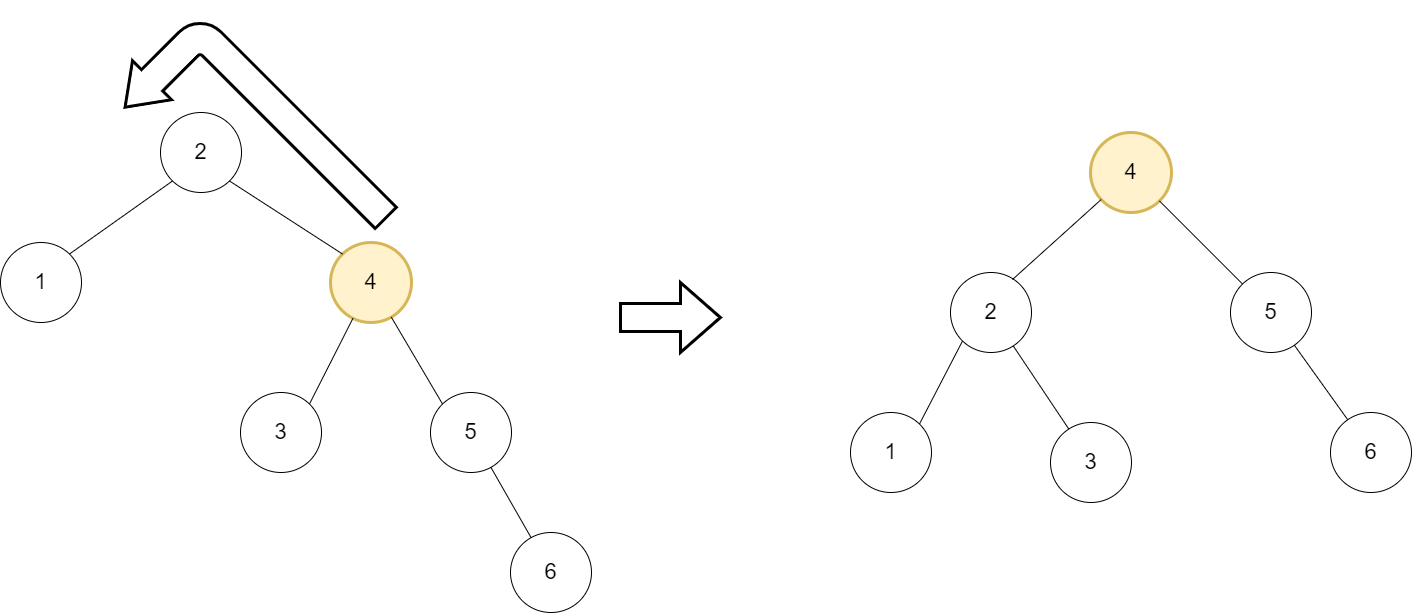
RL(Right Left)상태

- 오른쪽 서브트리 내의 왼쪽 서브트리가 가장 깊을 때 발생
- 해결책: 5번 노드를 Right연산 후 4번 노드를 Left연산을 수행

LR상태과 RL상태를 해결하기 위해선 LR연산과 RL연산을 수행한다. 이때 연산 과정을 보면 서브트리의 루트 노드를 회전연산을 통해 LL혹은 RR상태로 만드는 것을 볼 수 있다. 즉 LR, RL상태일 때는 LL상태 혹은 RR상태를 만들고 이를 해결하는 방식으로 동작된다고 이해할 수 있다.
AVL트리가 워낙 유명하다보니 시뮬레이터도 있다. 궁금하면 직접 삽입, 삭제연산을 수행하여 동작을 수행하는 과정을 보는 것도 좋다.
https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
'CS' 카테고리의 다른 글
| [Network] http (0) | 2022.12.04 |
|---|---|
| [자료구조] 해시맵 (0) | 2022.07.13 |
| [자료구조] 트리 개론 (0) | 2022.07.04 |
| [Web]CORS (1) | 2022.06.20 |
| [GoF] 2. Factory (0) | 2022.03.22 |
